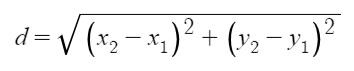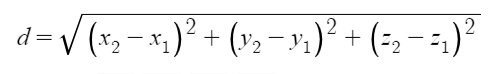Posted on

Staying Sharp

When I first made the transition from working in industry as a firmware engineer to teaching high school, my technical skills earned through my education and work experience was a selling point in interviews. One thing I’ve worried about during my teaching career so far is “losing my edge.” I’ve had the thought that the longer I spend as a teacher and not working in my field, the more likely I am to lose skills or knowledge I once had. Maybe this fear is irrational, but I’ve taken some steps to prevent it.

Formal Education

The most straightforward action I’ve taken is to take graduate courses in computer science. During my first couple years teaching I was an advisor for seniors so I spent time looking into different university programs. At the same time I was investigating the requirements to teach dual credit courses. To my dismay and amusement, I was qualified to teach computer science both at the high school and university level but not dual credit (teaching a class that gives both high school and college credit). I had a B.S. in Computer Science and an M.A. in Secondary Education but I needed at least 18 hours at the graduate level in my subject to teach dual credit.

Eventually I found Georgia Tech’s Online Masters of Science in Computer Science (OMSCS) program which appealed to me for many reasons such as the low price tag, completely online nature, awarding the same degree as the on-campus equivalent without any special “online” designation and a wide range of interesting courses available. I’ve gotten to brush up in some areas like databases, artificial intelligence and information security, take classes relevant to my career as an educator like education technology and human-computer interaction and explore new topics I wasn’t exposed to in undergrad like machine learning. I feel like I’m getting to double dip: I’m learning content as a student in the program and I’m paying close attention to how these courses are run to think more about my own pedagogical practices.

Reading

I love learning from books. There are many must-reads like Code by Charles Petzold, Clean Code by Robert C. Martin, and The C Programming Language by Kernighan & Ritchie (even if C is the primary language you use). Not only do well established, popular books contain valuable knowledge and insights but it gives you common language to use when discussing technical matters with others.

I also enjoy reading more recently written books even if they center around a technology or tool that might not be around (or widely used) in a few years. A book that I attribute to pushing me to pursue computer science as a teenager was the book Game Programming for Teens which taught the basics of Game Programming using a language called BlitzBasic which I haven’t used or heard anyone talk about since I used it during my reading of that book. There’s still lots to be gained from the experience of using specific tools even if you move on to something else later on. Recently, I read a book about using Design Patterns in Unity 2019. I quickly jumped into Game Program Patterns by Robert Nystrom which is excellent.

I also try to diversify what I read. A good book that got me thinking more about ethical considerations of emerging technology was Weapons of Math Destructions by Cathy O’Neil. And there’s more to read than just books. There’s a ton to learn from articles online and blogs. I particularly like seeing blogs from other CS teachers like Mike Zamansky and Alfred Thompson.

Sharing

In addition to reading what other people have to say, sharing what I have to offer has been crucial in my personal development as well. Writing about my experiences in a blog has been a good way to stop and reflect and get something more out of those experiences.

I also share links to things I’m working on on social media like twitter. So far, I usually don’t get much feedback but the little I’ve received has been quite useful. I’ve thought about making an explicit ask of specific people to take a look and give me feedback since it is so valuable. I also understand that it’s a significant ask so I want to not do it too often and try to offer something of value to the community in return.

Something I have only done a couple times but would like to do more of is giving talks at conferences. At LexPlay (Game convention in Central Kentucky), I shared some experience using video games as a mode of learning with some fellow teachers. I also gave two talks (one regular and one “lightning”) at PyCon Thailand. One was about teaching with Python. The other was about using programming skills to help with language learning (It was only 5 minutes but I gave that talk in Thai which was pretty terrifying but worthwhile). I also showed off a game I made at the Louisville Arcade Expo which was an incredibly fun way to showcase a project I had made. Something I’ve recently begun is streaming myself working on some of my projects on sites like Twitch and YouTube. Even if there are few or no viewers, it helps me to talk through my process out loud as if I were explaining it to someone else.

Side Projects

I think probably the most important thing I’ve done to keep developing my programming skills is… programming. Time is a precious commodity. So, spending time outside work hours working on side projects can be tough but enjoyable if it’s something you’re really into. I have also spent planning time during the school day working on relevant projects like demos for students and tools like random name generators, group selection helpers and programming challenges with automated tests on repl.it.

Outside of work I’ve participated in game jams like Global Game Jam, made a Thai language learning app for Android and just generally fiddled around with tools like p5js, codepen.io and Unity. By trying to use tools I’m unfamiliar with I can experience the pain of setting up new and sometimes confusing software just like my students do. I also get to experience the joy of finally getting things to work.

Teaching a variety of courses

There are definitely pros and cons of teaching a large number of courses. It would be nice to have a semester teaching multiple sections of the same course or teaching the same courses for several years in a row to be able to reduce the workload and time spent on planning, curriculum design and creating assessments and rubrics but there’s a benefit to constantly changing it up as well.

I’ve only been teaching for 5 years but I’ve already taught Computational Thinking, Computer Programming, Web Development, Robotics, Design Technology, and IB Computer Science (Year 1 and 2, Standard Level and Higher Level). In addition to IB I’ve taught under the Common Core in the U.S. and British Columbia curriculum in a Candian overseas school.

I feel that I get a chance to learn as I review code that students produce. I have gotten better at paying attention to detail. I have to make robust tests since students will create all sorts of unpredictable code that could pass simple tests but still be incorrect. I have to learn common misconceptions and anticipate them.

I’ve been teaching math too: Algebra I and II, Geometry, Precalculus and Calculus. Every new topic I teach, I feel I get a deeper understanding of the content and I grow in my ability to relate a wide variety of topics to students. I try to make connections between and within content and to the outside world. In my math classes I always try to sneak some computer science in and in my CS classes I sneak math in.

Collaboration

In addition to combining CS and Math content in the classes I teach personally, I’ve found that I get even more out of cross-curricular work when collaborating with teachers in different content areas. I no longer have an expert view of the whole problem domain, I have to learn to work with others to create something better than either of us could’ve done alone.

I’ve worked with an English teaching colleague to have students develop Choose-Your-Own-Adventure stories in HTML in our Web Development class. They also made Mad Libs in PHP and Buzzfeed style Top 10 lists populated with data from student created mysql databases. They used CSS to style their projects to help convey theme and mood.

I’ve collaborated with a Physics teacher to create visualizations and we got our students working together to make physics simulations for their final projects where my students made sure the simulations worked properly and allowed for customization of parameters while her students were the content experts and made sure the physics concepts were portrayed accurately.

Conclusion

A common theme in all of the ways I’ve tried to grow as a computer scientist and as an educator is that I always try to stay curious and try to go outside my comfort zone doing and learning new things. I try to put my learner hat on and not take myself too seriously. It’s also important to always step back and reflect to get the most out of every experience and to celebrate the successes along the way. I love what I do and I look forward to continuing to explore more topics over the years and sharing my accumulated expertise with others.

Posted on

Collision Detection

I recently read a great explanation of the Gilbert-Johnson-Keerthi Distance Algorithm for Efficient Collision detection. I highly recommend checking it out. I’ve used collision detection as a way of teaching both math and computer programming concepts to students for a few years and would love to share some of the examples I’ve made with other educators and students.

What is Collision Detection?

I suppose, first I should explain what collision detection is. It’s basically checking to see if two shapes are overlapping at all:

Why would we care if two shapes are colliding or not? Well, there are several situations where this information is important: in video games to see if the player is being hit by an enemy, in physics simulations to check if two objects are bumping into one another or in robotics when interpreting sensor data.

Circles

Now that the answer to the “But, when are we gonna use this in the REAL world?” question is out of the way, how do we actually do it? Let’s just consider circles for now. What information do we need to figure out if two circle are colliding? See if you can figure it out by playing with the example below. Note that r1 and r2 are the radii of the circles.

What was the relationship between the distance and the sum of the radii when the circle are colliding? We can represent it in pseudocode:

if (distance < r1 + r2) then
circles are colliding
else
circles are not colliding
end if

Your inner mathematician might be saying “If they are equal, the circles intersect at a point, they should be colliding!” That’s fine, change the “less than” in the code above to a “less than or equal to” but with how floating point arithmetic works, it should be functionally equivalent. The only reason you can get the distance to equal 75 above is because I rounded the actual value to avoid the ugliness of a ton of numbers after the decimal point. Edge cases like that make for good classroom discussion.

To draw the circles to the screen we need to already know the radius and location of the center of each circle. But we will have to compute the distance ourselves. If you know the center of circle 1 is at (x1, y1) and the center of circle 2 is at (x2, y2) we can use the Pythagorean Theorem (or distance formula) to find the distance.

If we wanted to express that in pseudocode, we do something like:

dx = x2 - x1
dy = y2 - y1
distance = sqrt( dx*dx + dy*dy )

Above I used intermediate values of dx and dy to represent the difference in the x values and the difference in the y values. This isn’t required. We could have made this a one-liner but for the sake of clarity, I broke it down into multiple steps. I also just multiplied dx by itself to square it even though some languages have an exponentiation operator (** in python) or a power function like Math.pow().

Cool, that’s about all there is to that example. If you want to play around with the code yourself, here you go.

Spheres

I told you that collision detection is used in video games but aren’t more and more video games being made in 3D nowadays? We just looked at circles which are 2D. Let’s see if we can extend our approach to work in 3D by considering two spheres instead of two circles. This next toy has sliders to control the position of one of the spheres in the x, y and z direction. Try to make them collide. What information do we need to figure out if they are colliding? No numbers on screen provided this time:

You may have realized that the information we need is identical: the radius of each sphere and the distance between them. The same general method stated in the 2D case works for the 3D case. Of course, this time we’ve now got to consider the position of each sphere in the z direction. But luckily, we don’t have to tweak our distance formula very much to make it work:


Or, in pseudocode:

dx = x2 - x1
dy = y2 - y1
dz = z2 - z1
distance = sqrt( dx*dx + dy*dy + dz*dz )

if (distance < r1 + r2) then
spheres are colliding
else
spheres are not colliding
end if

For a good explanation of why this is, check out Math is Fun. But if tinkering with code sounds more fun to you, here it is.

Rectangles

Alright, 2D, 3D, we’ve got this! But, what if we want other shapes like rectangles or cubes? No radius in a rectangle, so our above method wouldn’t work. But, circles alone won’t always cut it. Consider the following situation:

With bounding circles, we might get a false positive and think two objects are colliding when they aren’t. You could shrink the circles around them to reduce the number of false positives but then you’d end up with false negatives:

Sometimes, rectangles will just be a better fit than circles for the objects we want to enclose. So, let’s try to figure out how to tell if two rectangles are colliding.


If you want spoilers, see how I did it in the code.

Unfortunately, there’s not an elegant mathematical formula like the Pythagorean Theorem that can help us out this time. We’ve got to do some logical deduction and come up with a set of rules. It may be easier to thinking about one dimension at a time.

In the diagram above, we see that we can draw the two line segments such that A is always to the left of B and C is to the left of D. The question of collision becomes about the relationship of the points on the red segment to the points on the blue segment. The rule to me seems to be that if A is to the left of D and B is to the right of C, the segments collide. This holds for these 3 examples. Try coming up with more and see if that rule holds or if you can find an exception.
The next challenge is to extend this from 1D to 2D.


In this diagram, imagine you’re only seeing one side of a rectangle for each of the given line segments. For two of the pairs, you could draw rectangles that would be colliding but for the first, you can’t. Try it if you don’t believe me.

Now, rotate these examples 90 degrees. You will see that the same rule above can tell us whether the projections of a rectangle onto either the x-axis or the y-axis collide. We have to combine all that to form a single conjunctive logical rule (by that, I mean several comparisons connected with “and”).


When drawing rectangles in code, you might have 4 points but more likely you just have one point (most commonly, the top left corner) and the width and height of the rectangle. We can still figure out the other points from that information give that these rectangles are axes aligned. For example, the bottom right corner of the first rectangle would be (x1+w1, y2+h2) and the top right corner of the second rectangle is (x2+w2, y2). This is enough information to allow us to write some pseudocode:

if (x1 < x2 + w2)
and (x1 + w1 > x2)
and (y1 < y2 + h2)
and (y1 + h1 > y2) then
rectangles are colliding
else
rectangles are not colliding
end if

This will likely take more work to convince yourself it’s true than the circles and spheres. Come up with examples, see if you can find any that this code fails on.

Many collisions

In a game or a simulation, it’s likely there are more than two objects on the screen at a time. So, we need to be able to take the concepts above and apply them repeatedly in a given scene. The example below isn’t interactive like the rest but keep an eye on how quickly the number of collisions adds up:


(As always, feel free to play with the code. Try changing the 3 values at the top and seeing what happens.)

One way you could handle all these collisions is by using an array to store all the objects and a loop to iterate through them all and another loop nested inside of that to check like this:

N = 15
circles = new Array(N)
//add circles to the array
index1 = 0
loop from 0 to N - 1
start = index1 + 1
index2 = index1 + 1
loop from start to N - 1
//check if circle[index1] is colliding with circle[index2]
index2 = index2 + 1
end loop
index = index + 1
end loop

That’s a lot of collision checks. The first circle is checked against the other N – 1 circles, then the 2nd circle is checked against the remaining N – 2 and so on. Another math connection here: arithmetic sequences and series. If we add it up, there would be (N2 – N) / 2 comparisons. There are definitely ways to do this more efficiently. If that interests you, you might want to investigate techniques like space partitioning.

This is a really fun topic to me. It’s rife with connections between math and computer science. There’s tons of possible extension and it can be used to create really fun projects. Most modern game engines will handle collision detection for you, but understanding how your tools work helps you get better at using them. I hope you enjoyed playing around with these examples as much as I enjoyed creating them.

All the examples in the post were written using p5.js, a javascript library meant to be accessible and used for creative expression. I made the diagrams using draw.io which will soon be changed to diagrams.net.