I recently read a great explanation of the Gilbert-Johnson-Keerthi Distance Algorithm for Efficient Collision detection. I highly recommend checking it out. I’ve used collision detection as a way of teaching both math and computer programming concepts to students for a few years and would love to share some of the examples I’ve made with other educators and students.
What is Collision Detection?
I suppose, first I should explain what collision detection is. It’s basically checking to see if two shapes are overlapping at all:

Why would we care if two shapes are colliding or not? Well, there are several situations where this information is important: in video games to see if the player is being hit by an enemy, in physics simulations to check if two objects are bumping into one another or in robotics when interpreting sensor data.
Circles
Now that the answer to the “But, when are we gonna use this in the REAL world?” question is out of the way, how do we actually do it? Let’s just consider circles for now. What information do we need to figure out if two circle are colliding? See if you can figure it out by playing with the example below. Note that r1 and r2 are the radii of the circles.
What was the relationship between the distance and the sum of the radii when the circle are colliding? We can represent it in pseudocode:
if (distance < r1 + r2) then
circles are colliding
else
circles are not colliding
end if
Your inner mathematician might be saying “If they are equal, the circles intersect at a point, they should be colliding!” That’s fine, change the “less than” in the code above to a “less than or equal to” but with how floating point arithmetic works, it should be functionally equivalent. The only reason you can get the distance to equal 75 above is because I rounded the actual value to avoid the ugliness of a ton of numbers after the decimal point. Edge cases like that make for good classroom discussion.
To draw the circles to the screen we need to already know the radius and location of the center of each circle. But we will have to compute the distance ourselves. If you know the center of circle 1 is at (x1, y1) and the center of circle 2 is at (x2, y2) we can use the Pythagorean Theorem (or distance formula) to find the distance.
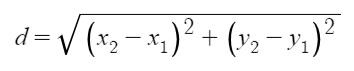
If we wanted to express that in pseudocode, we do something like:
dx = x2 - x1
dy = y2 - y1
distance = sqrt( dx*dx + dy*dy )
Above I used intermediate values of dx and dy to represent the difference in the x values and the difference in the y values. This isn’t required. We could have made this a one-liner but for the sake of clarity, I broke it down into multiple steps. I also just multiplied dx by itself to square it even though some languages have an exponentiation operator (** in python) or a power function like Math.pow().
Cool, that’s about all there is to that example. If you want to play around with the code yourself, here you go.
Spheres
I told you that collision detection is used in video games but aren’t more and more video games being made in 3D nowadays? We just looked at circles which are 2D. Let’s see if we can extend our approach to work in 3D by considering two spheres instead of two circles. This next toy has sliders to control the position of one of the spheres in the x, y and z direction. Try to make them collide. What information do we need to figure out if they are colliding? No numbers on screen provided this time:
You may have realized that the information we need is identical: the radius of each sphere and the distance between them. The same general method stated in the 2D case works for the 3D case. Of course, this time we’ve now got to consider the position of each sphere in the z direction. But luckily, we don’t have to tweak our distance formula very much to make it work:
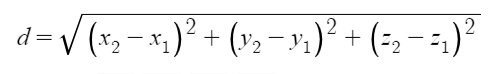
Or, in pseudocode:
dx = x2 - x1
dy = y2 - y1
dz = z2 - z1
distance = sqrt( dx*dx + dy*dy + dz*dz )
if (distance < r1 + r2) then
spheres are colliding
else
spheres are not colliding
end if
For a good explanation of why this is, check out Math is Fun. But if tinkering with code sounds more fun to you, here it is.
Rectangles
Alright, 2D, 3D, we’ve got this! But, what if we want other shapes like rectangles or cubes? No radius in a rectangle, so our above method wouldn’t work. But, circles alone won’t always cut it. Consider the following situation:
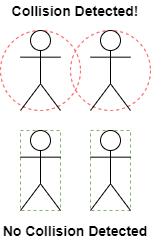
With bounding circles, we might get a false positive and think two objects are colliding when they aren’t. You could shrink the circles around them to reduce the number of false positives but then you’d end up with false negatives:
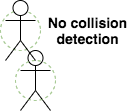
Sometimes, rectangles will just be a better fit than circles for the objects we want to enclose. So, let’s try to figure out how to tell if two rectangles are colliding.
If you want spoilers, see how I did it in the code.
Unfortunately, there’s not an elegant mathematical formula like the Pythagorean Theorem that can help us out this time. We’ve got to do some logical deduction and come up with a set of rules. It may be easier to thinking about one dimension at a time.
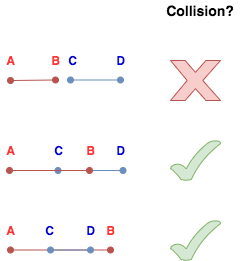
In the diagram above, we see that we can draw the two line segments such that A is always to the left of B and C is to the left of D. The question of collision becomes about the relationship of the points on the red segment to the points on the blue segment. The rule to me seems to be that if A is to the left of D and B is to the right of C, the segments collide. This holds for these 3 examples. Try coming up with more and see if that rule holds or if you can find an exception.
The next challenge is to extend this from 1D to 2D.
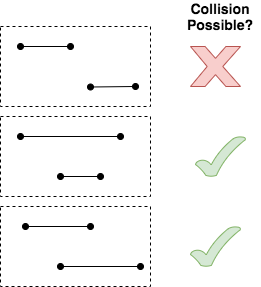
In this diagram, imagine you’re only seeing one side of a rectangle for each of the given line segments. For two of the pairs, you could draw rectangles that would be colliding but for the first, you can’t. Try it if you don’t believe me.
Now, rotate these examples 90 degrees. You will see that the same rule above can tell us whether the projections of a rectangle onto either the x-axis or the y-axis collide. We have to combine all that to form a single conjunctive logical rule (by that, I mean several comparisons connected with “and”).
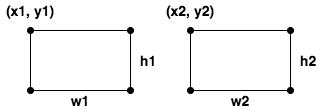
When drawing rectangles in code, you might have 4 points but more likely you just have one point (most commonly, the top left corner) and the width and height of the rectangle. We can still figure out the other points from that information give that these rectangles are axes aligned. For example, the bottom right corner of the first rectangle would be (x1+w1, y2+h2) and the top right corner of the second rectangle is (x2+w2, y2). This is enough information to allow us to write some pseudocode:
if (x1 < x2 + w2)
and (x1 + w1 > x2)
and (y1 < y2 + h2)
and (y1 + h1 > y2) then
rectangles are colliding
else
rectangles are not colliding
end if
This will likely take more work to convince yourself it’s true than the circles and spheres. Come up with examples, see if you can find any that this code fails on.
Many collisions
In a game or a simulation, it’s likely there are more than two objects on the screen at a time. So, we need to be able to take the concepts above and apply them repeatedly in a given scene. The example below isn’t interactive like the rest but keep an eye on how quickly the number of collisions adds up:
(As always, feel free to play with the code. Try changing the 3 values at the top and seeing what happens.)
One way you could handle all these collisions is by using an array to store all the objects and a loop to iterate through them all and another loop nested inside of that to check like this:
N = 15
circles = new Array(N)
//add circles to the array
index1 = 0
loop from 0 to N - 1
start = index1 + 1
index2 = index1 + 1
loop from start to N - 1
//check if circle[index1] is colliding with circle[index2]
index2 = index2 + 1
end loop
index = index + 1
end loop
That’s a lot of collision checks. The first circle is checked against the other N – 1 circles, then the 2nd circle is checked against the remaining N – 2 and so on. Another math connection here: arithmetic sequences and series. If we add it up, there would be (N2 – N) / 2 comparisons. There are definitely ways to do this more efficiently. If that interests you, you might want to investigate techniques like space partitioning.
This is a really fun topic to me. It’s rife with connections between math and computer science. There’s tons of possible extension and it can be used to create really fun projects. Most modern game engines will handle collision detection for you, but understanding how your tools work helps you get better at using them. I hope you enjoyed playing around with these examples as much as I enjoyed creating them.
All the examples in the post were written using p5.js, a javascript library meant to be accessible and used for creative expression. I made the diagrams using draw.io which will soon be changed to diagrams.net.

